In the last post we introduced cyclic groups. The cyclic group Cn is generated by S, where S represents clockwise rotation through 360°/n (or 1/n of a revolution). It includes S2, which is 2/n of a revolution, and S3, which is 3/n of a revolution, and so on, all the way up to Sn-1. Notice that Sn = I is a complete revolution, which gets us back where we started.
More generally, suppose p is a whole number. Divide p by n to obtain the quotient q and remainder r. We can write p ÷ n = q R r or p = q ⋅ n + r. So Sp = Sqn+r = (Sn)q ∘ Sr. In other words, Sp consists of q complete revolutions composed with r/n of a revolution. It follows that Sp is the same as Sr. So, if we want to see what Sp does, we really only need to pay attention to the remainder of p ÷ n.
Suppose n = 8 for example. The group C8 is the group of rotations of the regular octagon, generated by a 45°-rotation S.
What transformation is (say) S29? Well, 29 ÷ 8 = 3 R 5, so S29 amounts to 3 complete revolutions composed with 5/8 of a revolution, or rotation through 5 ⋅ 45° = 225°. In other words, S29 = S5.
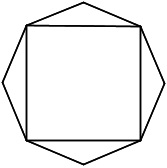
Now, we’ve noted that, if m is a divisor of n, then Cm is contained within Cn. This can be seen in the following way. Write n = m ⋅ q. Then Sq represents 1/m of a revolution. For instance, if n = 8, then we can take m = 4. Writing 8 = 4 ⋅ 2, we see that S2 represents one quarter of a revolution, i.e., a rotation through 90°.
This observation amounts to the following fact: a regular polygon with m sides can be inscribed in a regular polygon with n sides if and only if m is a divisor of n. (We regard a line segment as a “polygon” with two sides.) To draw the polygon with m sides, connect every qth vertex, where n = m ⋅ q.
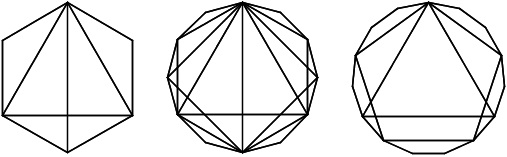
For instance, the divisors of 6 are 2 and 3, so we can inscribe an equilateral triangle and a bisecting line segment in a regular hexagon. The triangle is constructed by connecting every second vertex. Or again, the divisors of 12 are 2, 3, 4, and 6, so we can inscribe a hexagon, a square, an equilateral triangle, and a bisecting line segment in the regular dodecagon. The square is constructed by connecting every third vertex, since 12 = 4 ⋅ 3.
The divisors of 15 are 3 and 5, so we can inscribe a regular pentagon and an equilateral triangle in the regular pentadecagon. The pentagon is constructed by connecting every third vertex, since 15 = 5 ⋅ 3.
So, if m is a divisor of n with n = m ⋅ q, then 〈Sq〉 = Cm. We’d like to answer the more general question now: If p is any whole number, then what does the group 〈Sp〉 amount to? In other words, if we keep composing p/n of a revolution with itself, what cyclic group do we obtain?
Let’s consider the example of n = 8 again. Take p = 3, and write T = S3. Then T is a 135°-rotation, or 3/8 of a revolution. Let’s start composing T with itself. To begin with, T2 is 6/8 of a revolution, or S6. Then T3 is 9/8 of a revolution, which is the same as 1/8 of a revolution. So T3 = S. Next, T4 is 12/8 of a revolution, which is the same as 4/8 of a revolution, or S4. Continuing like this, we find that the group generated by T consists of I, S3, S6, S, S4, S7, S2, and S5, in that order. So 〈T〉 = C8.
Now let’s take p = 6. Write U = S6. The group generated by U consists of S6, S4, S2, and I. We don’t obtain the entire group in this case. In fact, since S6 is a 270°-rotation, S4 is a 180°-rotation, and S2 is a 90°-rotation, we see that 〈U〉 = C4.
If we check each of the elements of C8, what we’ll find is the following. The group can be generated by each of S, S3, S5, and S7. The transformations S2 and S6 only generate C4. The transformation S4 generates C2. And the transformation I generates the trivial group C1.
Now, if p and n are whole numbers not both zero, then their greatest common divisor d is the largest whole number that divides both p and n. For instance, the greatest common divisor of 6 and 8 is 2, while the greatest common divisor of 12 and 30 is 6. In general, the group generated by Sp is the same as the group generated by Sd where d is the greatest common divisor of n and p. So, writing n = m ⋅ d, we find that 〈Sp〉 = Cm. If p and n share no common divisors larger than 1, then they are said to be relatively prime; in this case, m = n, and Sp generates the whole cyclic group.
Consider the case n = 12. Then S, S5, S7, and S11 each generate C12 since 12 shares no common divisors larger than 1 with 1, 5, 7, or 11. The transformations S2 and S10 each generate C6 since the greatest common divisor of 12 and 2, or 12 and 10, is 2. The transformations S3 and S9 each generate C4 since the greatest common divisor of 12 and 3, or 12 and 9, is 3. The transformations S4 and S8 generate C3. The transformation S6 generates C2. And I generates C1.
Or again, consider n = 15. Then S, S2, S4, S7, S8, S11, S13, and S14 each generate C15. Next, S3, S6, S9, and S12 each generate C5. The transformations S5 and S10 generate C3. And I generates C1.
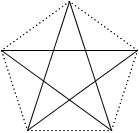
Pick a single vertex of the n-sided polygon. Imagine repeatedly applying a rotation Sp to it (where p is less than n) and connecting each pair of consecutive points with a line segment. This amounts to connecting every pth vertex. If p happens to be 1 or n – 1, then we obtain the polygon itself. But if p is between 1 and n – 1, then we obtain either an inscribed polygon or a star. Also, the figure produced by p is the same as that produced by n – p; the direction is just reversed. It should also be clear that an inscribed star has n points if and only if p and n are relatively prime.
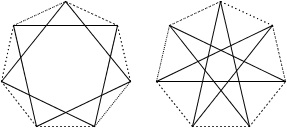
Everyone knows that there’s one 5-pointed star; this corresponds to p = 2 (or p = 3), because we draw it by connecting every second (or third) vertex.
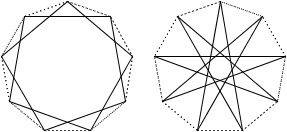
Next, there are no 6-pointed stars because each of 2, 3, and 4 share common divisors with 6. But there are two 7-pointed stars, corresponding to p = 2 (or p = 5) and p = 3 (or p = 4).
We draw the first by connecting every second vertex, and the second by connecting every third vertex. There is only one 8-pointed star, corresponding to p = 3 (or p = 5).
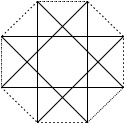
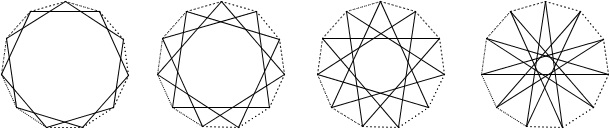
It’s drawn by connecting every third vertex. If we connect every second vertex, we wind up with a square; if we connect every fourth vertex, we obtain a bisecting line segment. Next, there are two 9-pointed stars, corresponding to p = 2 (or p = 7) and p = 4 (or p = 5).
In general, if n happens to be a prime number, hence has no divisors other than 1 and itself, then there are (n – 3)/2 different n-pointed stars. For instance, there are (11 – 3)/2 = 4 different 11-pointed stars.